電子は粒子としての性質を示すだけでなく波動としての性質も示します。 ここでは電子を波動、つまり波として考える必要があります。 そもそも波とは何でしょうか？身近なところでは海の波がすぐに思い浮かぶと思います。 目に見える光も波です。目には見えませんがテレビやラジオの電波も波です。 それではこれら波が持つ性質を簡単に見ていきましょう。

波とは振動が次々に隣へと伝わっていくものです。波の模式図を下に示しています。

図を見てもわかるように波は上から下へ、そしてまた上から下へと振動しています。 ここで波の一つのサイクルの長さを波長と呼びます。 例えばラジオの波長なら、その長さは数百メートルもあります。 目に見える光、可視光線で波長は10万分の数センチメートル程度です。

次に波と波がぶつかるとどうなるのか見てみましょう。その図を下に示しています。

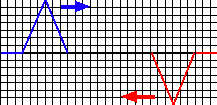
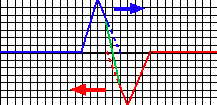
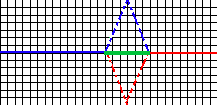
上図のように波は互いに影響し合います。波の山と谷がぶつかるとお互いに打ち消し合います。 図中では青波と赤波がぶつかった時にできる波を緑で書いています。

電子の場合も波として考えると、電子の波の山と谷が重なるような条件では打ち消しあって 電子が存在できなくなると言えます。これと反対に、電子の波の山と谷が重ならない条件ならば 電子は存在できることになります。この条件を満たすところが電子殻となるところです。

電子が安定して存在できるの条件は、波の山と谷が重なりあわない ことです。波の性質として 一波長だけ進むとまた元の振幅に戻ります。これより、波の経路が 波長の整数倍であれば波が何周しようとも山と谷が重なることはありません。 それではこの条件を式で書いて見ます。 原子の半径をr、電子の波長をλ(ラムダ)とすると次の式が成り立ちます。
2πｒ=nλ(n=1,2,3,4・・・)
この時nは常に整数です。1.3などの小数にはなりません。

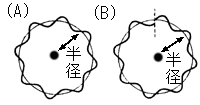
左図は水素原子の中の電子の状態を示しています。 上の式が成り立っているときの状態が(A)の時です。 (A)では波の山と谷の部分がぶつからないため打ち消し合ってしまうことはありません。

反対に成り立たないときの状態が(B)です。 (B)の状態では山と谷がぶつかり、いずれ互いを打ち消しあってしまいます。 だから電子は安定に存在できなくなってしまうのです。

このように電子はどこにでも存在できるわけではなく、電子が存在できる領域が 限定されます。このように電子が存在できる領域を電子殻と言います。